Kinship matrix
A kinship matrix (K), sometimes also referred to as matrix G, or genetic relationship matrix, is a variance-covariance (vcv) matrix, the ones we usually use in the randome effects part of mixed models. Therefore, the dianogals is within-individual variance, which is represented by the degree of homozygosity or inbreeding level. Actually, the diagnoals are 1 + F, where F is the inbreeding coefficient as descirbed in a previous post about HWE. The offdiagnals are covariance between pairs of individuals. If you are not familiar with covariance, check out this previous post.
Kinship matrices can be calcuated based on different kind of information: pedigree, DNA markers and/or sequence data.
A matrix
If a kinship matrix is estimated using pedigree info, it is called a A matrix, A for additive. Sometimes it is also referred to as numerator relationship matrix (numerator/demoninator) and I have a theory of where the name is coming from later in the post. Traditionally, before we had molecular data, kinship matrices can only be estimated using pedigrees information, therefore it is the expected genetic relationships between individuals in a population. It is supposed to captures the probability that two alleles in two individuals are identical by descent (IBD).
GRM
If a kinship matrix is estimated using genome sequencing, it is called a Genomic Relationship Matrix (GRM). See their differences summarized below:
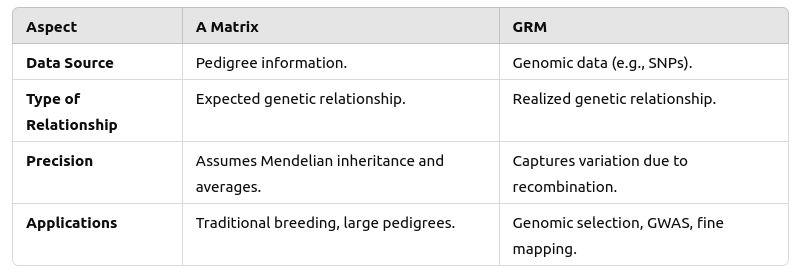
Computation of A matrix
Short Version
There are R packages with ready-built functions to calculate the pedigree from the .fam file of plink. One is the kinship2::pedigree.
# read in your .fam file as fam
colnames(fam) <- c("FID", "IID", "PID", "MID", "Sex", "Phonotype")
ped <- with(fam, pedigree(id = IID, dadid = PID, momid = MID, sex = Sex, famid = FID))
This works for animals. However this won’t work if you have selfing in your dataset since it is not possible to set the sex for the individual. Because it would be both the PID and MID for its offsprings, there is no correct way to set the sex column for it. If you set it to be 1(male), it will complain that Id not female, but is a mother. Therefore you also cannot set it to be 2 (female). You also cannot set it to be 0(unknown) then it will still complain that it is a mother/father. In this case you can use nadiv. Pretty funny that here the dadid and momid is specified as dam and sire, so animals, but it only gives warning for selfing ones, and it gives selfing ones 1 for its relationship to itself.
library(nadiv)
ped <- data.frame(
id = fam$IID,
dam = fam$MID, # mother; NA if unknown
sire = fam$PID, # father; NA if unknown
stringsAsFactors = FALSE
)
ped_ordered <- prepPed(ped)
# yeah, selfing is allowed!
A_matrix <- as.matrix(makeA(ped_ordered))
Long Version (by hand)
Here we will follow the R code in Austin Putz’s post for A matrix computation by hand.
# create original pedigree
ped <- matrix(cbind(c(3:6), c(1,1,4,5), c(2,0,3,2)), ncol=3)
# change row/col names
rownames(ped) <- 3:6
colnames(ped) <- c("Animal", "Sire", "Dam")
# print ped
print(ped)
This won’t work because in a pedigree, every one in 2nd and 3rd column (parents), needs to be in the first column (we need to know the parents of everyone). Now we have 1,2,3,4,5 in the 2nd and 3rd column, but only 3,4,5 are in the first column, which means we need to add 1 and 2 in the first column. If we do not know their parents, just use 0. Note that pedigree needs to be sorted from oldest (top) to youngest (bottom), meaning parents goes before offsprings.
ped <- matrix(cbind(c(1:6), c(0,0,1,1,4,5), c(0,0,2,0,3,2)), ncol=3)
# change row/column names
rownames(ped) <- 1:6
colnames(ped) <- c("Animal", "Sire", "Dam")
# print matrix
print(ped)
Then it gives the logic for generating the A matrix. Basically you need to generate the off-diagnal first. The relationship between individual 1 and individual 2 is defined as the average relationship between individual 1 and the parents of individual 2:
a_ind1,ind2=0.5(aind1,sire2 + aind1,dam2).
After you have the off-diagnals, the diagnals are easy:
a_diag=1+0.5(a_sire,a_dam), and since everything in the sire and dam are in column 1, (a_sire, a_dam) is one of the off-diagnal.
The only thing that is in the way is the 0s, when the parents info is unknown.
Let’s look at the code.
createA <-function(ped){
if (nargs() > 1 ) {
stop("Only the pedigree is required (Animal, Sire, Dam)")
}
# This is changed from Gota's function
# Extract the sire and dam vectors
s = ped[, 2]
d = ped[, 3]
# Stop if they are different lengths
if (length(s) != length(d)){
stop("size of the sire vector and dam vector are different!")
}
# set number of animals and empty vector
n <- length(s)
N <- n + 1
A <- matrix(0, ncol=N, nrow=N)
# set sires and dams (use n+1 if parents are unknown: 0)
s <- (s == 0)*(N) + s
d <- (d == 0)*N + d
start_time <- Sys.time()
# Begin for loop
for(i in 1:n){
# equation for diagonals
A[i,i] <- 1 + A[s[i], d[i]]/2
for(j in (i+1):n){ # only do half of the matrix (symmetric)
if (j > n) break
A[i,j] <- ( A[i, s[j]] + A[i, d[j]] ) / 2 # half relationship to parents
A[j,i] <- A[i,j] # symmetric matrix, so copy to other off-diag
}
}
# print the time it took to complete
cat("\t", sprintf("%-30s:%f", "Time it took (sec)", as.numeric(Sys.time() - start_time)), "\n")
# return the A matrix
return(A[1:n, 1:n])
}
The first thing to notice is that it starts as a n+1 by n+1 matrix filled with 0. This means unknown relationships are by default 0 unless changed later.
Secondly, it fills by the order of a11, a12, a13 all the way to a16, then a22, a23 to a26, etc. This is why the ordering from old to young is so important. Because the eldest ones are the ones with unkown parents, therefore a11 is always 1 (a77 is 0, 7 for unknown).
Now that we have the A matrix, how do we understand those numbers intuitively?
On the off diagnal:
- “0.5”: a13, a14 and a23 they are parent-offspring, 50% heritance. a15, 1 is the father of 3 and 4, and 5 is the child of 3 and 4, so still 50%.
- “0.25”: a16 = (a1,5 + a1,2)/2 = ((a1,4 + a1,3)/2 + a1,2)/2 = ((0.5 + 0.5)/2 + 0)/2 = 0.25.
- “0”: a12, a24: a12 = (a1,7 + a1,7)/2 = 0. a24=(a2,1 + a2,7)/2 = (0+0)/2 = 0
On the diagnal:
- “1”: a11, a22 and a44: they all have one or two 0 in their parents info, theirfore (a_sire, a_dam) is always 0.
- “1”: a33 = 1 + 0.5 * (a12),
- “1.125”: a55 and a66. This is still in the diagnal, a55=1+0.5 * a34. a34 = (a13 + a37)/2 = (0.5+0)/2, so a55=1+0.5 * 0.25 = 1.125. Same with a66. But What does it mean by exceeding 1? Can think about this in terms of uneven variance in the general least square case.
Since we know A matrix is vcv matrix where the diagnals are not always 1, you can turn it into relationships(similarities) by dividing the off-diagonal elements by the square roots of the product of the cooresponding diagonals. This is called taking a covariance matrix and reducing it to a correlation matrix. Recall that correlation is standardized covariance.
There is a equation for it:
# convert A to actual relationships
A_Rel <- correlateR::cov2cor(A)
# print matrix
print(round(A_Rel, 4))
How it works is that eventually everything on the diagonal becomes 1. The ones on the offdiagonal are scaled by its related variance. for example, a1,2 will be scalled by a11 an a22: a12_new = a12_old/sqrt(a11 * a22). I think this is why the A matrix is called the numerator relationship matrix since its elements go above the division bar.
Indeed when you use the rrBLUP::A.mat(SNP_matrix), the diagnals in the matrix that is returned are not just ones. You can scale it by A = A/mean(diag(A)). This function basically does transposed cross product of the SNP_matrix. therefore a GBLUP model where Z=SNP_matrix is equivalent to K=A.mat(SNP_matrix).
OK I hope know you understand what is happening. The original post is much better than mine!